Pavimentações...

   A pavimentação de um plano equivale simplesmente a conseguir cobri-lo com figuras planas, de modo a não existirem espaços entre elas e sem haver sobreposições. Dadas certas figuras geométricas, pode utilizar-se a matemática para decidir previamente se será possível a pavimentação, sem ser necessário colocar as figuras. Para o descobrir é necessário saber que a amplitude angular da circunferência é de 360º.

Armados desta ferramenta e de algum conhecimento geométrico, consideremos a pavimentação de um chão com pentágonos regulares. Um pentágono regular tem cinco lados e cinco ângulos congruentes (geometricamente iguais). Para se achar a medida do ângulo interno do pentágono, decompomo-lo em triângulos, tal como é ilustrado. Em qualquer triângulo, a soma das amplitudes dos ângulos internos é 180º. Os cinco triângulos que formam o pentágono são congruentes, uma vez que os lados e os ângulos correspondentes também o são. Podemos agora determinar a medida da amplitude dos ângulos do pentágono como sendo 108º. Assim, quando tentamos colocar os pentágonos regulares e congruentes lado a lado, descobrimos que tem de existir um espaço entre eles, porque os ângulos dos pentágonos não podem formar um círculo (108º + 108º + 108º = 324º).

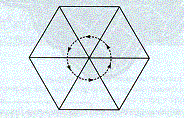
    Tentando agora pavimentar o chão, utilizando triângulos equiláteros. Cada um dos triângulos equiláteros mede 60º. Podemos observar que é possível colocar seis triângulos equiláteros congruentes, de modo a completarem o círculo.

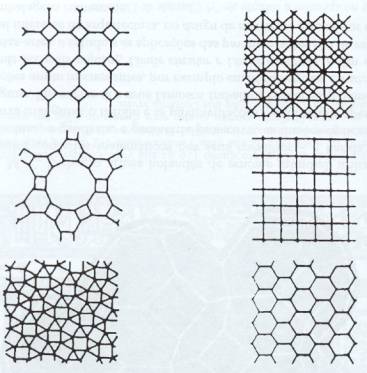
   E se utilizarmos quadrados, hexágonos, octógonos? Eis algumas pavimentações do plano:

Retirado do livro: Fascínios da Matemática – A Descoberta da Matemática que nos rodeia.

Autor: Theoni Pappas